Algoritmos iterativos
Antes de buscar un algoritmo iterativo resaltemos de nuevo un detalle importante. Aunque estamos hablando de varios algoritmos, la solución óptima (la de menos movimientos, que como hemos visto antes, para n = 8 es de 255) es única. O sea, la serie de movimientos que resulta de aplicar un algoritmo (óptimo) cualquiera será siempre la misma.Una observación clave para encontrar un algoritmo iterativo es que el disco más pequeño se mueve una vez sí, una vez no. El primer movimiento hay que hacerlo con el disco 1. Está claro que después de mover el disco 1 (en cualquier ocasión) se debe mover un disco distinto (si no queremos perder el tiempo moviendo el mismo disco varias veces). Este movimiento debe hacerse entre los dos postes que no contienen el disco 1. A continuación no nos quedan más que dos alternativas: deshacer el último movimiento, lo que no tiene sentido, o volver a mover el disco 1. Además, cuando le toque le toque el turno a un disco distinto de 1, el movimiento estará perfectamente determinado ya que sólo intervendrán dos postes, y entre dos postes sólo hay un movimiento posible. Así que sólo puede haber duda cuando hay que mover el disco menor. Se sale de esta duda respetando una cualquiera de las siguientes reglas.
- El disco pequeño se debe mover siempre cíclicamente en el mismo sentido: hacia la derecha (de A a B, de B a C y de C a A) o hacia la izquierda (de A a C, de C a B y de B a A), según el número de discos sea par o impar respectivamente.
- El disco pequeño se debe colocar siempre, bien sobre un disco de número par, bien como único disco en el poste de destino (C) si el número de discos es impar o en el otro (B) si es par.
- Si n es par, mueve el disco 1 hacia la derecha. Si es impar, muévelo hacia la izquierda.
- Si todos los discos están en C, fin. Si no, mueve un disco que no sea el 1 y vuelve al paso 1.
- Si es posible, lleva el disco 1 sobre un disco de número par. Si no es posible, llévalo al poste B si n es par o a C si n es impar.
- Si todos los discos están en C, fin. Si no, mueve un disco que no sea el 1 y vuelve al paso 1.

fig. 1
- Lleva el disco 1 sobre un disco (o trozo de base) que no sea de su mismo color.
- Si todos los discos están en C, fin. Si no, mueve un disco distinto de 1 y vuelve al paso 1.
Los movimientos de cada disco
Analizando otra vez el algoritmo recursivo y el razonamiento que nos llevó a él podemos comprobar que (centrándonos en el caso de 8 discos) el disco 8 se mueve una sola vez, el 7 dos veces, el 6 cuatro veces, etc. El disco 1 se mueve 128 veces. La suma de estas potencias de 2 coincide con el total de movimientos antes calculado (1 + 2 + 4 + 8 + 16 + 32 + 64 + 128 = 255). En general, el disco k se mueve 2n−k veces, y 20 + 21 + ... + 2n−1 = 2n−1.Vamos ahora a fijarnos en los momentos concretos en que se mueve cada disco. Para empezar trataremos el caso de cinco discos que en esta ocasión pintaremos con cinco tonos de azul.

fig. 2

fig. 3

fig. 4

fig. 5

fig. 6

fig. 7

fig. 8
Esta distribución de movimientos tiene una estrecha relación con la de unos y ceros en la secuencia de números binarios. Estos son los primeros 32 números (del 0 al 31, todos los que se pueden escribir con cinco dígitos, o más precisamente con cinco bits) en codificación binaria, ordenados por columnas.
00000 01000 10000 11000 00001 01001 10001 11001 00010 01010 10010 11010 00011 01011 10011 11011 00100 01100 10100 11100 00101 01101 10101 11101 00110 01110 10110 11110 00111 01111 10111 11111tabla 1
Tanto el primer número (00000 no lo tenemos en cuenta) como el último terminan en 1 y entre un número que termina en 1 y el siguiente hay sólo otro separándolos.
El primer número terminado en 10 es 00010, ocupando el segundo (el 10º, en notación binaria) lugar de la lista. El último es 11110, también segundo, pero contando por el final. Entre un número terminado en 10 y el siguiente hay 3 = 22−1 (100−1 en binario).
El primer número terminado en 100 es 00100, el cuarto (el 100º, en notación binaria) de la lista. El último es 11100, cuarto contando por el final. Entre un número terminado en 100 y el siguiente hay 7 = 23−1 (1000−1 en binario).
Igual que hicimos antes con la tira de cuadros (pero en sentido inverso) podríamos seguir hasta el quinto dígito. En general, en la lista de los primeros 2n−1 números binarios (sin contar el 0) usaremos n dígitos (bits). Para cualquier k entre 1 y n, el primer número terminado en un 1 seguido de k−1 ceros está a 2k−1−1 del principio y el último está a la misma distancia del final; entre cualquier número de esta forma y el siguiente hay una separación de 2k−1. En definitiva, estos unos marcados en negrita en la lista indican qué disco interviene en cada movimiento de la Torre de Hanoi. Un ejemplo, volviendo a la torre de ocho discos. Supongamos que queremos saber qué disco se mueve en el movimiento 136. En binario y usando 8 bits, 136 se escribe 10001000, así que se mueve el disco 4, ya que el primer bit con valor uno contando de derecha a izquierda es el cuarto.
La dirección de los movimientos
Ya que sabemos qué disco se mueve en cada momento, veamos ahora si podemos determinar hacia dónde. Como ya hicimos antes al hablar del algoritmo de Buneman y Levy, consideraremos que el poste A está a la derecha del poste C, así que si un disco está en C y decimos que se mueve hacia la derecha, irá a para a A. Análogamente, un disco en A que se mueve hacia la izquierda irá a parar a C.En primer lugar, el disco n realiza un solo movimiento hacia la izquierda, como se aprecia en la figura 2 (porque hemos fijado el poste de destino en C; en caso contrario iría hacia la derecha). El disco n−1 se mueve primero de A a B y después a C, desplazándose en ambos casos hacia la derecha. Se ve en la siguiente animación (disco 7).

fig. 9
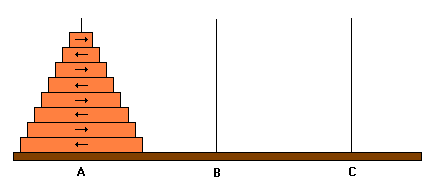
fig. 10
Estamos en condiciones de escribir un tercer algoritmo iterativo basado en los números binarios.
- Para m = 1 hasta m = 2n−1...
- Mueve el disco k en la dirección d, donde k es el lugar ocupado por el primer 1 que aparece en la forma binaria de m (contando de derecha a izquierda) y d es izquierda si n−k es par y derecha si n−k es impar.
La posición de los discos
Antes vimos que la representación binaria del número de cada movimiento de la solución nos mostraba qué disco se movía y en qué dirección. Ahora vamos a ver que es posible incluso determinar en qué poste se encuentra cada disco, de acuerdo con el método descubierto por Timothy R. S. Walsh. La idea es ir colocando los discos por orden decreciente de tamaño.La nueva idea clave es que el disco k se encuentra sobre el disco k+1 si, y sólo si, en la representación binaria del número de movimiento los bits k y k+1 (contando de derecha a izquierda) coinciden. Con esto y el hecho ya conocido de que sólo pueden estar en contacto discos de distinta paridad es posible ir colocando todos los discos. Si suponemos que las bases de los postes están los discos n+1, n+2 y n+3 no hace falta tratar el disco n como una excepción; estará en el poste inicial cuando el bit de la izquierda sea 0 y en el poste de destino cuando sea 1. Para mayor facilidad podemos colorear el puzzle como en la figura 4.
Por ejemplo, después del movimiento 136 (010001000), el disco 8 (010001000) no está sobre el «disco 9», es decir, sobre la base del poste inicial, así que tiene que estar sobre el 11 (la base del poste de destino). El disco 7 (010001000) no se encuentra encima del 8, así que, por paridad, tiene que estar sobre el 10 (base del poste B). El disco 6 (010001000) se encuentra sobre el 7, y el 5 (010001000) sobre el 6. El disco 4 (010001000) no está encima del 5, así que está en el poste A (no puede estar en C, porque tendría que colocarse encima del 8, que tiene la misma paridad). El disco 3 (010001000) no está sobre el 4, y por paridad está sobre el 8, en el poste C (arriba del poste B está 5, impar como 3). Para terminar, el disco 2 (010001000) está encima del 3 y el 1 (010001000) está encima del 2. La siguiente animación ilustra todo el proceso.

fig. 11
Saliéndose del camino
Hasta ahora nos hemos movido siempre dentro de la línea recta que une la posición inicial con la final, siguiendo una secuencia única de movimientos determinada desde el principio por el primer algoritmo. Pero las reglas del juego permiten otras posibilidades, por ejemplo, que haya discos juntos de la misma paridad. Es decir, hay muchos más movimientos y posiciones (o estados) que los vistos hasta ahora. Un estado queda definido por el poste donde está cada disco. Por ejemplo, en una torre de 3 discos, BCC sería el estado en el cual el disco 1 está en B, y los discos 2 y 3 están en C. Como en cada poste los discos están ordenados, esta información es suficiente.
fig. 12

fig. 13

fig. 14

fig. 15

fig. 16

fig. 17

fig. 18
Algoritmo pésimo para trasladar la torre 1...n del poste X al poste Z, usando como auxiliar el poste Y.
- Si n = 1, lleva el disco 1 primero de X a Y, y luego de Y a Z; fin.
- Traslada la torre 1...n−1 usando este mismo algoritmo, de X a Z, usando como auxiliar Y
- Lleva el disco n de X a Y.
- Traslada la torre 1...n−1 usando este mismo algoritmo, de Z a X, usando como auxiliar Y.
- Lleva el disco n de Y a Z.
- Traslada la torre 1...n−1 usando este mismo algoritmo, de X a Z, usando como auxiliar Y.

fig. 19
- Mueve el disco 1 dos veces hacia la derecha, primero de A a B y luego de B a C.
- Si todos los discos están en C, fin. Si no, mueve otro disco cualquiera (sólo habrá una posibilidad).
- Mueve el disco 1 dos veces hacia la izquierda, primero de C a B y luego de B a A.
- Mueve un disco distinto de 1 (sólo habrá una posibilidad) y vuelve al primer paso.
Cambiando la posición inicial
Normalmente se presenta la Torre de Hanoi con una posición inicial fija, pero nada impide que, al modo de otros famosos rompecabezas, como el Juego del 15 o el Cubo de Rubik, partamos de una posición aleatoria. Es como si nos dejaran en un punto cualquiera del grafo y tuviéramos que llegar a la meta (que sigue estando abajo a la derecha) por el camino más corto. El grafo de orden 3 será suficiente para ilustrarlo. Encuentra el camino desde el punto verde hasta el rojo por el camino más corto.
fig. 20

fig. 21

fig. 22
El siguiente algoritmo recursivo resuelve de forma óptima la Torre de Hanoi desde cualquier posición inicial. Llamaremos Z al poste de destino. En la última llamada n vale 0, en cuyo caso no hay que hacer nada (no se puede hacer nada con una torre de cero discos).
Algoritmo para formar la torre 1...n en el poste Z.
- Si n = 0, fin.
- Sea X el poste donde se encuentra el disco n. Si X = Z, forma la torre 1...n−1 (usando este mismo algoritmo) en Z y termina.
- Sea Y el poste que no es ni Z ni X. Forma la torre 1...n−1 en Y (usando este mismo algoritmo).
- Lleva el disco n de X a Z.
- Forma la torre 1...n−1 en Z (usando este mismo algoritmo, o bien otro de los vistos antes, puesto que la torre 1...n−1 ya está formada en Y).

fig. 23

tabla 2
La columna de la izquierda no ofrece ninguna duda: simplemente hay que poner la letra del poste donde se encuentra el disco cuyo número figura a la izquierda. Como el disco 4 está en el poste A en la primera casilla debemos poner una A. En la segunda casilla siempre debe ir una C. En las demás filas la columna «Va a...» se completa de la siguiente forma: si los dos valores de la fila anterior coinciden, se pone el mismo; si son distintos se pone la letra que falta. En este caso, por ejemplo, como tenemos en la primera fila A y C, hay que poner B. En la fila correspondiente al disco 2 hay que poner C en ambas columnas (porque el disco 2 está en el poste C y porque el poste distinto de A y B es C). El disco 1, por fin, se encuentra en B y va a C (mismo valor que el repetido en la fila anterior).
Una vez completada la tabla podemos hacer el primer movimiento, que corresponde a la primera fila, empezando por abajo, cuyas casillas son distintas. En este caso, el primer movimiento consiste en llevar el disco 1 del poste B al C. Después de hacer cada movimiento hay que actualizar la tabla a partir de la fila implicada en el movimiento. Como el movimiento era de la última fila (disco 1) sólo hay que cambiar ésta, poniendo el valor correcto para la columna «Está en...».
Ahora la primera fila (de abajo hacia arriba) con valores desiguales es la del disco 3, así que el segundo movimiento consiste el llevar el disco 3 del poste A al poste B. Pero esta vez la actualización de la tabla afecta a todas las filas a excepción de la primera. En el siguiente a movimiento vuelve a intervenir el disco 1.
Este proceso se repite hasta que todas las casillas de la tabla contienen una C.
Aunque este algoritmo es bastante adecuado para implementarlo en una computadora, ir escribiendo y borrando en un papel queda poco efectista cuando queremos impresionar a los amigos. Un algoritmo más apropiado para este fin se basa en las siguientes ideas, algunas ya familiares. La clave está en el tercer punto.
- En principio no sabemos si el primer movimiento lo debe realizar el disco 1 u otro, pero una vez determinado esto, al igual que ocurría en la solución clásica, se deben alternar movimientos con el disco 1 y con otro disco.
- Cuando le toca el turno a un disco distinto de 1, sólo hay un movimiento posible.
-
Salvo si es el primer movimiento, el disco 1 debe desplazarse según el
siguiente orden de preferencias.
- Sobre un disco par lo más pequeño posible.
- A un poste vacío.
- Sobre un disco impar lo más grande posible.
- Entre un disco par y otro impar elige el par.
- Entre dos discos pares elige el menor.
- Entre dos discos impares elige el mayor.
- Entre un disco par y un poste vacío elige el disco par.
- Entre un disco impar y un poste vacío elige el poste vacío.
- Determina el primer movimiento según el método explicado antes con la tabla.
- Si todos los discos están en el poste de destino, fin.
- Si el último movimiento ha sido con el disco 1, mueve un disco distinto (sólo hay una posibilidad). Si ha sido con otro disco, mueve el disco 1 según los criterios explicados antes. Vuelve al paso 2.
Si, como se hace a veces, el puzzle se presenta sin un poste final fijo (se trata de formar la torre en cualquier poste; en el grafo equivale a encaminarse hacia el vértice más cercano) se puede usar el siguiente algoritmo (no óptimo), que aparece en la respuesta del archivo de rec.puzzles.
- Llama 1 al poste que contiene al disco más pequeño (disco 1).
- Llama 2 al poste que contiene el disco más pequeño que no está en el poste 1. Si este disco es k, los discos 1...k−1 están formando una torre en 1 y k está en la cima de 2.
- Lleva los discos 1...k−1 del poste 1 al poste 2 (usando cualquiera de los algoritmos conocidos para trasladar una torre completa).
- Si no están todos los discos correctamente colocados, vuelve al paso 1.
Cambiando la posición final
Después de haber resuelto el rompecabezas cambiando la posición inicial, ¿nos atrevemos a cambiar también la posición final? Realmente, un ligero cambio en el algoritmo de la tabla que vimos antes resuelve también este caso totalmente general. Basta tener en cuenta el destino de cada disco, que no será necesariamente el poste C. Al principio hay que poner en la segunda casilla el destino del disco n. Una vez colocado este disco habrá que poner el destino que le corresponda a n−1 en la cuarta casilla, etc.Vamos a mostrarlo con el mismo ejemplo de antes, pero cambiando la posición final, que ahora será AACB. El siguiente dibujo alterna entre la posición inicial y la final si hacemos clic con el ratón sobre él.

fig. 24

tabla 3
- B → A
- C → B
- A → B
- A → C
- B → A
- B → C
- A → C
- A → B
- C → B
- C → A
- B → A